Vizualizare şi simulare īn MAPLE

Exemple

 

 

Studenţi:   Marian-Silviu Tălmăcel
                 Oana-Adriana Basarabă
                 Cristian-Laurenţiu Giorgi
                 Roxana-Elena Stăniloiu
Īndrumător: conf. dr. Mădălina Buneci

 

 

1. Introducere

 

        “O imagine valorează mai mult decāt 1000 de cuvinte”.  Acesta este un principiu pe care oamenii de ştiinţă īl folosesc de secole pentru a transmite informaţii despre concepte ştiinţifice, date şi modele.

Scopul acestei lucrări este de exemplifica folosirea mediului Maple pentru vizualizarea şi simularea unor fenomene legate de aplicarea metodelor numerice. Mai precis lucrarea constă īn crearea unor proceduri Maple pentru vizualizarea/simularea metodelor bisecţiei şi tangentei (pentru rezolvarea ecuaţiilor neliniare) şi pentru aproximarea funcţiilor prin polinoame de interpolare.

Pentru claritate la īnceputul fiecărei secţiuni s-a prezentat pe scurt metoda pentru care s-au creat proceduri de vizualizare/simulare.

 

2.  Rezolvarea ecuaţiilor

           Presupunem date a, bĪR, f: [a,b] ® R. Problema pe care o studiem este determinarea numerelor reale xĪ[a,b] cu proprietatea că f(x) = 0. Numim un număr real x*Ī[a,b] cu proprietatea că f(x*) = 0, soluţie (sau rădăcină) a ecuaţiei f(x) = 0.

Dacă f : [a,b] ® R, este o funcţie continuă cu proprietatea că

f(a)f(b) < 0, atunci există cel puţin o rădăcină x* Ī(a,b) a ecuaţiei f(x) = 0. Rădăcina ecuaţiei f(x) = 0 nu este neapărat unică.

           

2.1. Metoda bisecţiei

Fie f : [a,b] ® R, o funcţie continuă cu proprietatea că  f(a)f(b) < 0. Atunci există cel puţin o rădăcină x* Ī(a,b) a ecuaţiei f(x)=0. Pentru găsirea rădăcinii se micşorează la fiecare pas intervalul īn care funcţia īşi schimbă semnul. Metoda bisecţiei presupune īnjumătăţirea la fiecare pas a acestui interval. Astfel:

·        se determină mijlocul c = (a + b)/2 al intervalului (a,b).

·        dacă f(c)f(a)<0, atunci se continuă algoritmul cu intervalul [a,c]

·        dacă f(c)f(b)<0, atunci se continuă algoritmul cu intervalul [c,b]

·        dacă f(c) =0 s-a determinat o rădăcină a ecuaţiei f(x) = 0.

         Se construieşte astfel un şir de intervale (In)n , In = [an, bn], cu lungimea lui In egală cu jumătate din lungimea lui In-1. Fiecare din aceste intervale conţine o soluţie a ecuaţiei f(x) = 0. Presupunem că se dă o precizie e>0.

         Considerăm că cn mijlocul intervalului In este o aproximaţie satisfăcătoare a soluţiei ecuaţiei f(x) = 0 dacă lungimea lui In este mai mică decāt e. Dacă notăm Ln = |bn - an| lungimea intervalului In, avem Ln = Ln-1/2 = ... = L0/2n = |b-a|/2n. Ca urmare Ln < e dacă şi numai dacă |b-a| /2n < e sau echivalent n > ln(|b-a|/e)/ln(2).

 

Algoritm

Date de intrare:

f continuă, a, b cu f(a)f(b)<0

e (precizie)

Date de ieşire:

            c mijlocul intervalului In  = [an, bn] cu | an-bn |<e (c este o aproximaţie a unei rădăcini x* Ī(a,b) a ecuaţiei f(x) = 0 cu eroarea absolută |x*-c| < e/2).

nmax:=[ln(|b-a|/e)/ln(2)] +1;

c: =(a+b)/2;

 

     pentru  j = 0, 1, ...., nmax execută

           

            dacă f(c) = 0 atunci  j : = nmax +1  

                        altfel               dacă  f(c)f(a)<0 atunci b : = c;  altfel a : = c;

                                    c: =(a+b)/2;

 

 

 

Rata convergenţei pentru metoda bisecţiei este liniară.

Propunem două variante de vizualizare a metodei.  Īn prima varianta se reprezintă grafic funcţia f: [a, b] ® R şi se marchează cu verde capetele inferioare ale intervalelor  [an, bn] şi cu albastru capetele superioare. Pentru fiecare cn: = (an + bn)/2 se marchează cu un cerculeţ punctul de pe grafic (cn, f(cn)). Procedura Maple de mai jos are drept parametrii funcţia f, capetele intervalului iniţial (notate A, B) şi precizia e.

 

> desen_bisectie:=proc(f,A,B,epsilon)

  local n,i,d1,d2,d3,c,a,b,an,bn,xn,j,nmax,titlu;

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`, intervalul [`,

  convert(A,string), `, `,convert(B,string),`], precizia `,

  convert(epsilon,string));

  a:=A;b:=B;

  an:=[a];bn:=[b];c:=(a+b)/2;xn:=[c];

  nmax:=floor(ln(abs(B-A)/epsilon)/ln(2))+1;

  for j from 0 to nmax do

  if f(c)=0 then j:=nmax+1 else

  if evalf(f(c)*f(a))<0 then b:=c;an:=[op(an),a];bn:=[op(bn),c];

  else a:=c;an:=[op(an),c];bn:=[op(bn),b]; fi; c:=(a+b)/2;

  xn:=[op(xn),c] fi  od;

  n:=nops(xn);titlu:=cat(titlu,`\nSe genereaza intervalele I[n] ce

  contin o solutie, n=1..`,convert(n,string), `\nverde=capatul inferior

  al intervalului I[n], albastru=capatul superior al intervalului I[n],

  j=1..`,convert(n,string));print(xn);

  d1:=plot(f(t),t=an[1]..bn[1],axes=normal,color=COLOR(RGB,1,0,0),

  labels=[X,Y],thickness=2,xtickmarks=map(evalf,xn));

  display(d1,display([seq(display(plot([[evalf(an[i]),t,t=min(0,

  evalf(f(an[i])))..max(0,evalf(f(an[i])))],[evalf(bn[i]),t,t=min(0,

  evalf(f(bn[i])))..max(0,evalf(f(bn[i])))]],

  color=[COLOR(RGB,0,1- i/(2*n),0),COLOR(RGB,0,0,1-i/(2*n))],

  thickness=1),pointplot([xn[i],f(xn[i])],symbol=CIRCLE,color=black,

  thickness=15)),i=1..n)],title=titlu))

  end;

 

       Pe graficele de mai jos vedem reprezentarea cu ajutorul procedurii desen_bisectie a aproximării prin metoda bisecţiei a soluţiilor ecuaţiilor: x8-3x-3 = 0 şi    (x+1)3 = 0.

> f1:=x-> x^8-3*x-3;

> f4:=x->(x+1)^3;

> desen_bisectie(f1,-3/2,1,10^(-3));

 

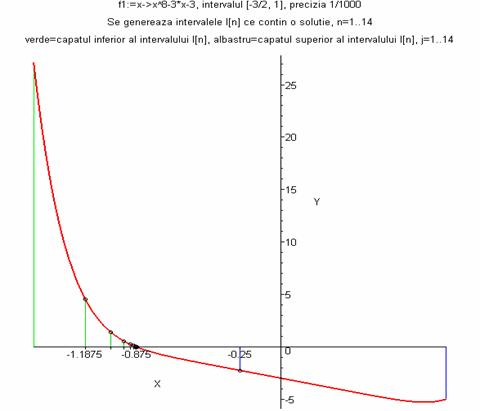
Lista

este lista mijloacelor intervalele generate (mijoacele intervalelor reprezintă aproximaţii ale rădăcinii ecuaţiei)

 

> desen_bisectie(f4,-2,1,10^(-3));

 

 

 

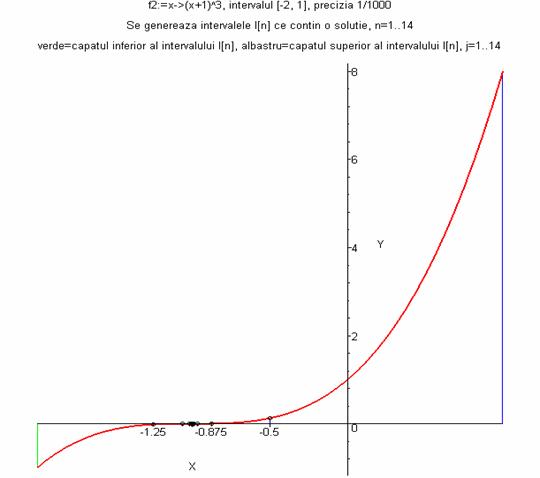
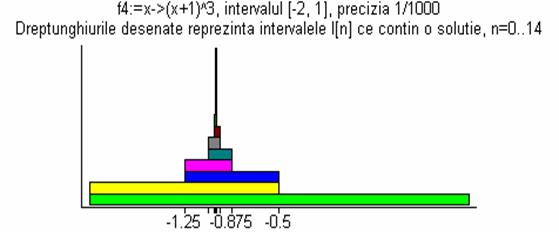
Īn cea de-a doua variantă se reprezintă cele [ln(|b-a|/e)/ln(2)] +1 intervale prin dreptunghiuri de culori diferite. Procedura desen_bisectie1 are aceiaşi parametrii ca desen_bisectie.

 

> with(plottools):

> desen_bisectie1:=proc(f,A,B,epsilon)

  local n,i,d1,d2,d3,c,a,b,abn,an,bn,xn,j, nmax,titlu;

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`, intervalul [`,

  convert(A,string), `, `,convert(B,string),`], precizia `,

  convert(epsilon,string));

  a:=A;b:=B; an:=[a];bn:=[b];c:=(a+b)/2;xn:=[c];

  nmax:=floor(ln(abs(B-A)/epsilon)/ln(2))+1;for j from 0 to nmax do

  if f(c)=0 then j:=nmax+1 else

  if evalf(f(c)*f(a))<0 then b:=c;an:=[op(an),a];bn:=[op(bn),c];

  else a:=c;an:=[op(an),c];bn:=[op(bn),b]; fi;

  c:=(a+b)/2; xn:=[op(xn),c] fi  od;

  n:=nops(xn);

  titlu:=cat(titlu,`\nDreptunghiurile desenate reprezinta intervalele

  I[n] ce contin o solutie, n=0..`,convert(n,string));

  abn:=seq([an[i],bn[i]],i=1..n); print(abn);

  display(seq(rectangle([an[i],i*0.1],[bn[i],(i+1)*0.1],

  filled=true,color=COLOR(RGB,(1-

  floor(log[5](i))/(floor(log[5](n))+1))*irem(irem(i,7)+1,2),(1-

  floor(log[5](i))/(floor(log[5](n))+1))*irem(iquo(irem(i,7)+1,2),2),(1-

  floor(log[5](i))/(floor(log[5](n))+1))*irem(iquo(irem(i,7)+1,4),2))),      

  i=1..n),axes=framed,title=titlu,xtickmarks=map(evalf,xn),

  ytickmarks=[]);

  end;

 

        Pe graficele de mai jos se pot observa intervalele In = [an, bn] obţinute prin aplicarea metodei bisecţiei (fiecare avānd lungimea egală cu jumătate din lungimea precedentului şi conţinānd o soluţie a ecuaţiei). Īnainte de reprezentarea grafică procedura desen_bisectie1 afişează şirul de intervale obţinut.

 

> desen_bisectie1(f1,-3/2,1,10^(-3),5);

 

 

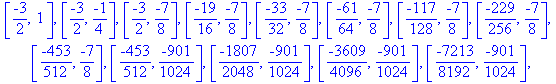
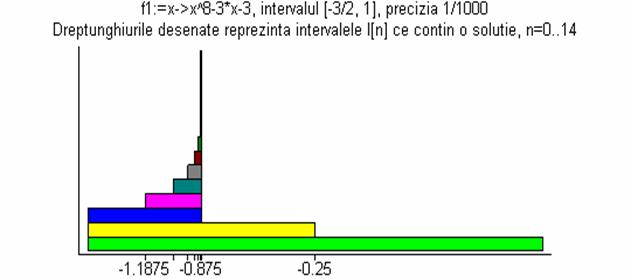
> desen_bisectie1(f4,-2,1,10^(-3),5);

 

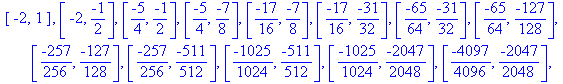
              Procedurile animatie_bisectie şi  animatie_desen_bisectie1 sunt variantele animate ale procedurilor desen_bisectie, respectiv desen_bisectie1. Procedura animatie_bisectie1 este o variantă a procedurii animatie_bisectie īn care, īn loc să se marcheze pe grafic punctul corespunzător aproximaţiei curente a rădăcinii, se uneşte cu linie punctată mijlocul intervalului curent de pe axa OX cu punctul corespunzător de pe grafic.

 

> animatie_bisectie:=proc(f,A,B,epsilon,m)

  local n,i,d1,d2,d3,c,a,b,an,bn,xn,j, nmax,titlu;

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`, intervalul [`,

  convert(A,string), `, `,convert(B,string),`], precizia `,

  convert(epsilon,string));

  a:=A;b:=B;

  an:=[a];bn:=[b];c:=(a+b)/2;xn:=[c];

  nmax:=floor(ln(abs(B-A)/epsilon)/ln(2))+1;

  for j from 0 to nmax do

  if f(c)=0 then j:=nmax+1 else

  if evalf(f(c)*f(a))<0 then b:=c;an:=[op(an),a];bn:=[op(bn),c];

  else a:=c;an:=[op(an),c];bn:=[op(bn),b]; fi;

  c:=(a+b)/2; xn:=[op(xn),c] fi  od;

  n:=nops(xn);titlu:=cat(titlu,`\nSe genereaza intervalele I[n] ce

  contin o solutie, n=1..`,convert(n,string), `\nverde=capatul inferior

  al intervalului I[n], albastru=capatul superior al intervalului I[n],  

  j=1..`,convert(n,string));print(xn);

  d1:=plot(f(t),t=an[1]..bn[1],axes=normal,color=COLOR(RGB,1,0,0),

  labels=[X,Y],thickness=2,xtickmarks=map(evalf,xn));

  display(d1,display([seq(display(plot([[evalf(an[i]),t,t=min(0,

  evalf(f(an[i])))..max(0,evalf(f(an[i])))],[evalf(bn[i]),t,t=min(0,

  evalf(f(bn[i])))..max(0,evalf(f(bn[i])))]],color=[COLOR(RGB,0,1,0),

  COLOR(RGB,0,0,1)]),pointplot([xn[i],f(xn[i])],symbol=CIRCLE,

  color=black,thickness=15))$m,i=1..n)],title=titlu,insequence=true))

  end;

 

 

> animatie_bisectie1:=proc(f,A,B,epsilon,m)

  local n,i,d1,d2,d3,c,a,b,an,bn,xn,j, nmax,titlu;

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`, intervalul [`,

  convert(A,string), `, `,convert(B,string),`], precizia `,

  convert(epsilon,string));

  a:=A;b:=B;

  an:=[a];bn:=[b];c:=(a+b)/2;xn:=[c];

  nmax:=floor(ln(abs(B-A)/epsilon)/ln(2))+1;

  for j from 0 to nmax do

  if f(c)=0 then j:=nmax+1 else

  if evalf(f(c)*f(a))<0 then b:=c;an:=[op(an),a];bn:=[op(bn),c];

  else a:=c;an:=[op(an),c];bn:=[op(bn),b]; fi; c:=(a+b)/2;

  xn:=[op(xn),c] fi  od;

  n:=nops(xn);

  titlu:=cat(titlu,`\nSe genereaza intervalele I[n] ce contin o solutie,

  n=1..`,convert(n,string), `\nverde=capatul inferior al intervalului

  I[n], albastru=capatul superior al intervalului I[n],

  j=1..`,convert(n,string));print(xn);

  d1:=plot(f(t),t=an[1]..bn[1],axes=normal,color=COLOR(RGB,1,0,0),

  labels=[X,Y],thickness=2,xtickmarks=map(evalf,xn));

  display(d1,display([seq(display(plot([[an[i],t,t=min(0,

  evalf(f(an[i])))..max(0,evalf(f(an[i])))],[bn[i],t,t=min(0,

  evalf(f(bn[i])))..max(0,evalf(f(bn[i])))]],labels=[X,Y],

  color=[COLOR(RGB,0,1,0),COLOR(RGB,0,0,1)],linestyle=[SOLID,SOLID],

  thickness=[2,2]),pointplot([[xn[i],0],[xn[i],f(xn[i])]],connect=true,

  linestyle=DOT,symbol=CIRCLE,color=black,thickness=1))$m,i=1..n)],

  title=titlu,insequence=true));

  end;

 

 

> animatie_desen_bisectie1:=proc(f,A,B,epsilon,m)

  local n,i,d1,d2,d3,c,a,b,abn,an,bn,xn,j, nmax,titlu;

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`, intervalul [`,

  convert(A,string), `, `,convert(B,string),`], precizia `,

  convert(epsilon,string));

  a:=A;b:=B;

  an:=[a];bn:=[b];c:=(a+b)/2;xn:=[c];

  nmax:=floor(ln(abs(B-A)/epsilon)/ln(2))+1;

  for j from 0 to nmax do

  if f(c)=0 then j:=nmax+1 else

  if evalf(f(c)*f(a))<0 then b:=c;an:=[op(an),a];bn:=[op(bn),c];

  else a:=c;an:=[op(an),c];bn:=[op(bn),b]; fi;

  c:=(a+b)/2; xn:=[op(xn),c] fi  od;

  n:=nops(xn);

  titlu:=cat(titlu,`\nDreptunghiurile desenate reprezinta intervalele

  I[n] ce contin o solutie, n=0..`,convert(n,string));

  abn:=seq([an[i],bn[i]],i=1..n);print(abn);

  display([seq(display(seq(rectangle([an[i],i*0.1],[bn[i],(i+1)*0.1],

  filled=true,color=COLOR(RGB,(1-

  floor(log[5](i))/(floor(log[5](n))+1))*irem(irem(i,7)+1,2),(1-

  floor(log[5](i))/(floor(log[5](n))+1))*irem(iquo(irem(i,7)+1,2),2),(1-

  floor(log[5](i))/(floor(log[5](n))+1))*irem(iquo(irem(i,7)+1,4),2))),

  i=1..j),axes=framed,title=titlu,xtickmarks=map(evalf,xn),

  ytickmarks=[]),j=1..n)],insequence=true);

  end;

 

Pentru exemplificare: click pe definiţia funcţiilor de mai jos

f1(x) = x8 – 3x -3

            f2(x) = ex+2x+1

            f3(x) =

            f4(x) = (x+1)3

            f5(x) = sin(x) + x  - 1

            f6(x) = sin(x)

 

2.2. Metoda tangentei

Metoda tangentei este utilizată pentru determinarea unei rădăcini a ecuaţiei f(x) = 0. Presupunem că f este derivabilă şi că derivata nu se anulează. Rădăcina ecuaţiei este determinată ca limita unui şir. Se pleacă de la un punct x0 dat. Presupunānd că s-a construit termenul xn-1, termenul xn se determină ca fiind abscisa intersecţiei dintre tangenta la graficul funcţiei īn xn-1 şi axa Ox.

 

 

 

 

 

 

 

 

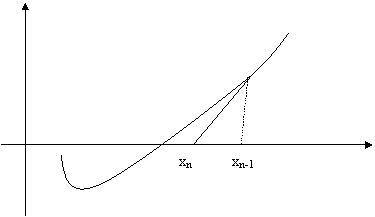
Ecuaţia tangentei īn (xn-1, f(xn-1)) este:

y – f(xn-1) = (xn-1)(x – xn-1)

Deci intersecţia cu axa Ox se află rezolvānd sistemul

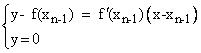
 Īn consecinţă ,

 

xn = xn-1 - .

 

Convergenţa şirului este determinată de termenul iniţial x0. Dacă x0 este īntr-o vecinătate suficient de mică a soluţiei atunci şirul converge. Următoarea teoremă stabileşte condiţii suficiente pentru convergenţa metodei tangentei.

 

Teoremă (Metoda tangentei). Fie f : [a, b] ® R o aplicaţie de două ori derivabilă cu următoarele proprietăţi: f’(x)¹0, f”(x) ¹ 0 oricare ar fi  xĪ[a, b] şi f(a)f(b)<0. Atunci unica soluţie x* a ecuaţiei f(x) = 0 este limita a şirului (xn)n definit prin:

xn = xn-1 - , n ³ 1

unde x0Ī [a, b] este ales astfel īncāt f(x0)f”(x0) > 0.  Īn plus, oricare ar fi n ³ 1 eroarea absolută cu care termenul xn aproximează x* verifică următoarele inegalităţi:

            |x* - xn| £

|x* - xn| £

unde m1 =  şi M2 = .

Algoritm

Date de intrare:

            f  - funcţia care determină ecuaţia (f(x) = 0)

            x0 -  aproximaţia iniaţială

            e >0 -precizia  (determină condiţia de oprire a iteraţiilor)

             Nmax numărul maxim de termeni din şir ce urmează a fi calculaţi (Nmax)

Date de ieşire: xN cu proprietatea că N este cel mai mic număr natural pentru care

| xn - xn-1 | < e sau n > Nmax

unde (xn)n­ este şirul corespunzător metodei tangentei (xN este considerat o aproximaţie satisfăcătoare a unicei soluţii a ecuaţiei f(x)=0)

            x1 := x0;

            x2 : = x1 -  ;

            n : = 1;

            cāt timp (| x2 – x1 | ³ e ) şi (n £ Nmax) execută

                        x1 := x2;

            x2 : = x1 - ;

            n : = n + 1;

                       

        Vom studia aproximarea soluţiilor a 4 ecuaţii diferite  prin această metodă.

ex+2x+1=0

(x+1)1/3=0

sin(x)+x-1=0

sin(x)=0

Procedura desen_mtangenta are ca parametrii funcţia f,  aproximaţia iniţială x0, precizia ε şi numărul maxim de termeni calculaţi – Nmax.

 

> desen_mtangenta:=proc(f,x0,epsilon,Nmax,m)

  local a,b,xn,x1,x2,n,df,titlu;

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`, aproximatia initiala

  x0=`, convert(x0,string),`,  precizia = `, convert(epsilon,string));

  df:=D(f); x1:=x0; xn:=[x1]; n:=0;x2:=x1-f(x1)/df(x1); xn:=[op(xn),x2];

  n:=n+1;

  while (evalf(abs(x2-x1))>=epsilon)and (n<Nmax) do

  x1:=x2;x2:=x1-f(x1)/df(x1);xn:=[op(xn),x2];n:=n+1 od; n:= nops(xn);

  titlu:=cat(titlu,`\nSe deseneaza cu albastru tangentele la grafic in

  punctele (x[n], `,f,`(x[n])), n=0..`,convert(n-2,string)); 

  print(xn);

  a:=min(seq(xn[i],i=1..n))-2*epsilon;

  b:=max(seq(xn[i],i=1..n))+2*epsilon;

  display(plot(f(t),t=a..b,color=COLOR(RGB,1,0,0),thickness=2, 

  labels=[X,Y],xtickmarks=map(evalf,xn)),display([seq(

  display(pointplot([[xn[i],0],[xn[i],f(xn[i])]],connect=true,

  symbol=CIRCLE,thickness=1,linestyle=DOT,

  color=COLOR(RGB,0,0,0))$(3*m),

  pointplot([[xn[i+1],0],[xn[i],f(xn[i])]],connect=true,thickness=1,

  linestyle=SOLID, color=COLOR(RGB,0,0,1)))$m,i=1..n-1)],title=titlu))

  end;

Aplicăm procedura următoarelor funcţii

> f2:=x->exp(x)+2*x+1;

> f3:=x->surd(x+1,3);

> f5:=x->sin(x)+x-1;

> f6:=x->sin(x);

Exemplificările au fost alese pentru a evidenţia diverse fenomene ce pot apărea.

> desen_mtangenta(f2,4.,10^(-3),10);

 

 

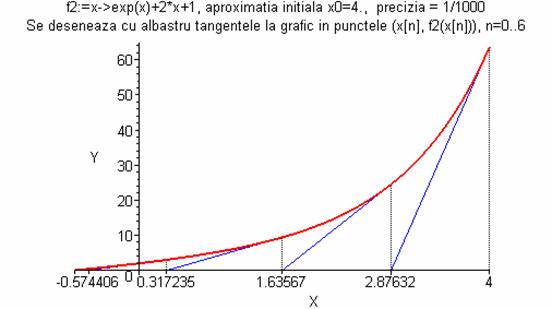
Pe graficul de mai sus observăm cum şirul construit prin metoda tangentei converge rapid către soluţia ecuaţiei ex+2x+1=0.

> desen_mtangenta(f3,-3.,10^(-3),10);

 

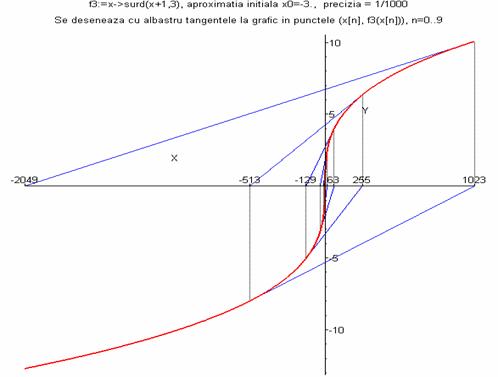
De această dată observăm că şirul construit prin metoda tangentei nu converge la soluţia ecuaţiei (x+1)1/3=0   (funcţia nu este derivabilă īn -1)

> desen_mtangenta(f5,2.51,10^(-3),10);

 

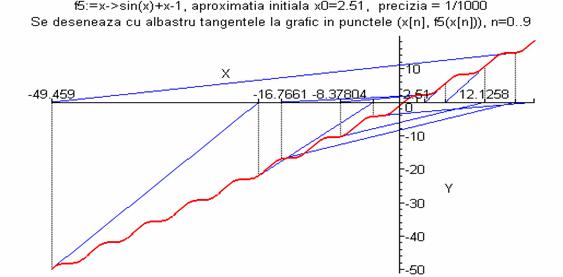
   Se observă că termenii şirului construit prin metoda tangentei se depărtează de soluţie, īnsă dacă luăm un număr mai mare de aproximări (Nmax), termenii şirului converg către soluţie.

> desen_mtangenta(f5,2.51,10^(-3),50);

 

 

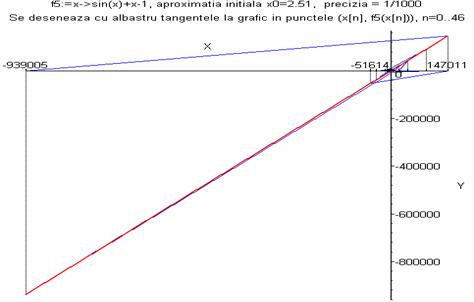
> desen_mtangenta(f6,1.41,10^(-3),10);

 

 

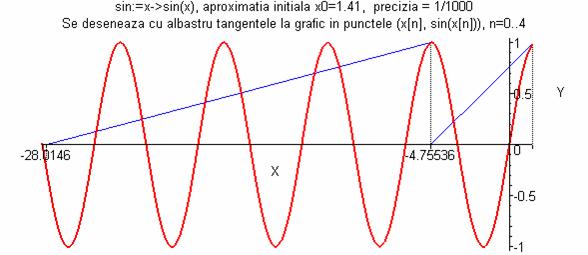
Pentru ecuaţia sin(x)=0 şirul construit prin metoda tangentei converge către soluţie, dar nu către cea mai apropiată (dacă aproximaţia iniţială este luată īn vecinătatea unui punct īn care se anulează funcţia cos).

Prezentăm două variante animate ale procedurii desen_mtangenta. Procedura animatie_mtangenta generează n cadre, īn fiecare cadru i fiind desenat graficul funcţiei şi tangenta la grafic īn punctul (xi, f(xi)).Parametrul suplimentar, m, este utilizat drept factor de īncetinire.

 

> animatie_mtangenta:=proc(f,x0,epsilon,Nmax,m)

  local a,b,xn,x1,x2,n,df,titlu;

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`, aproximatia initiala

  x0=`, convert(x0,string),`,  precizia = `, convert(epsilon,string));

  df:=D(f); x1:=x0; xn:=[x1]; n:=0;x2:=x1-f(x1)/df(x1);

  xn:=[op(xn),x2]; n:=n+1;

  while (evalf(abs(x2-x1))>=epsilon)and (n<Nmax) do

  x1:=x2;x2:=x1-f(x1)/df(x1);xn:=[op(xn),x2];n:=n+1 od;

  n:= nops(xn);

  titlu:=cat(titlu,`\nSe deseneaza cu albastru tangentele la grafic in

  punctele (x[n], `,f,`(x[n])), n=0..`,convert(n-2,string));  print(xn);  

  a:=min(seq(xn[i],i=1..n))-2*epsilon;

  b:=max(seq(xn[i],i=1..n))+2*epsilon;

  display(plot(f(t),t=a..b,color=COLOR(RGB,1,0,0),thickness=2,

  labels=[X,Y],xtickmarks=map(evalf,xn)),display([seq(display(

  pointplot([[xn[i],0],[xn[i],f(xn[i])]],connect=true,symbol=CIRCLE,

  thickness=1,linestyle=DOT, color=COLOR(RGB,0,0,0))$(3*m),

  pointplot([[xn[i+1],0],[xn[i],f(xn[i])]],connect=true,thickness=1,

  linestyle=SOLID, color=COLOR(RGB,0,0,1)))$m,

  i=1..n-1)],title=titlu,insequence=true))

  end;

 

       Procedura animatie_mtangenta1 generează n cadre, īn fiecare cadru i fiind desenat graficul funcţiei şi tangentele la grafic īn punctele (xj, f(xj)) pentru j=1..i. Parametrul suplimentar, m, este utilizat drept factor de īncetinire.

 

> animatie_mtangenta1:=proc(f,x0,epsilon,Nmax,m)

  local d,a,b,xn,x1,x2,n,df,titlu;

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`, aproximatia initiala

  x0=`, convert(x0,string),`,  precizia = `, convert(epsilon,string));

  df:=D(f); x1:=x0; xn:=[x1]; n:=0;x2:=x1-f(x1)/df(x1);

  xn:=[op(xn),x2]; n:=n+1;

  while (evalf(abs(x2-x1))>=epsilon)and (n<Nmax) do

  x1:=x2;x2:=x1-f(x1)/df(x1);xn:=[op(xn),x2];n:=n+1 od;

  n:= nops(xn);

  titlu:=cat(titlu,`\nSe deseneaza cu albastru tangentele la grafic in

  punctele (x[n], `,f,`(x[n])), n=0..`,convert(n-2,string)); 

  print(xn); a:=min(seq(xn[i],i=1..n))-2*epsilon;

  b:=max(seq(xn[i],i=1..n))+2*epsilon;

  d:=plot(f(t),t=a..b,color=COLOR(RGB,1,0,0),thickness=2,

  labels=[X,Y]);display(d,display([seq(display([seq(display(

  pointplot([[xn[i],0],[xn[i],f(xn[i])]],connect=true,symbol=CIRCLE,

  thickness=1,linestyle=DOT, color=COLOR(RGB,0,0,0)),

  pointplot([xn[i],f(xn[i])],symbol=CIRCLE,

  thickness=15,color=COLOR(RGB,0,1,0)),pointplot([[xn[i+1],0],

  [xn[i],f(xn[i])]],connect=true,thickness=1,

  linestyle=SOLID, color=COLOR(RGB,0,0,1))),i=1..j)])$m,

  j=1..n-1)],title=titlu,insequence=true))

  end;

 

Pentru exemplificare: click pe definiţia funcţiilor de mai jos

f1(x) = x8 – 3x -3

            f2(x) = ex+2x+1

            f3(x) =

            f4(x) = (x+1)3

            f5(x) = sin(x) + x  - 1

            f6(x) = sin(x)

 

3. Polinoame de interpolare

 

Fie x0, x1, …, xn n+1 puncte distincte două cāte două din intervalul  [a, b] (numite noduri), şi fie yi = f(xi) pentru orice i = 0,1,…n. Se numeşte polinom de interpolare asociat nodurilor x0, x1, …, xn şi valorilor y0=f(x0), y1= f(x1), …, yn=f(xn) un polinom Pn care īndeplineşte următoarele condiţii

                                    grad(Pn) £ n

Pn(xi) = yi, i = 0, 1, …, n .

Polinomul determinat de condiţiile anterioare există şi este unic. Polinomul de interpolare asociat nodurilor x0, x1, …, xn şi valorilor y0, y1, …, yn poate fi scris sub forma

Ln(x) =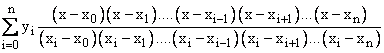

numită formă Lagrange.

Următoarea procedură are drept parametrii o listă x de noduri distincte două cāte două,  o listă y de valori şi un punct a. Procedura īntoarce valoarea īn a a polinomului de interpolarea asociat nodurilor din lista x şi valorilor din lista y. Polinomul de interpolare este calculat utilizānd scrierea lui sub forma Lagrange.

 

> polinom_Lagrange:=proc(x,y,a)

  local n,v,t,i,j;

  n:=nops(x);v:=0;

  for i from 0 to n-1 do

  t:=y[i+1];

  for j from 0 to i-1 do

  t:=t*(a-x[j+1])/(x[i+1]-x[j+1]) od;

  for j from i+1 to n-1 do

  t:=t*(a-x[j+1])/(x[i+1]-x[j+1]) od;

  v:=v+t;

  od;

  RETURN(v)

  end;

 

Eroare de interpolare. Comparaţie īntre nodurile echidistante şi nodurile Cebīşev

 

Teorema următoare stabileşte eroarea cu care polinomul de interpolare Pn aproximează funcţia f:

            Teoremă (eroarea de interpolare).  Fie f : [a, b] ® R o funcţie de clasă Cn+1. Fie x0, x1, …, xn n+1 puncte distincte două cāte două din intervalul  [a, b], şi yi = f(xi) pentru orice i=0,1,…n. Fie Pn polinomul de interpolare asociat nodurilor x0, x1, …, xn şi valorilor y0=f(x0), y1= f(x1), …, yn=f(xn). Atunci oricare ar fi xĪ[a,b], există zxĪ(a,b) astfel īncāt

f(x) – Pn(x) =  (x – x0) (x – x1) … (x – xn).

Īn consecinţă, oricare ar fi x Ī [a, b], avem:

| f(x) – Pn(x) | £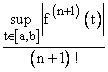 |(x – x0) (x – x1) … (x – xn)|.

 

Fiind dat un interval [a, b], x0, x1, …, xn se numesc noduri echidistante din intervalul  [a, b] dacă

xi­ = a + ih, i = 0, 1, ...n,    h = .

Īn cazul nodurilor echidistante se poate arăta că eroarea de interpolare satisface:

| f(x) – Pn(x) | £  pentru orice xĪ[a, b].

 

Pentru n Ī N dat, se numesc noduri Cebīşev (rădăcini ale polinomului Cebīşev de prima speţă de grad n+1) numerele reale:

xi = , 0 £ i £ n.

Polinoamele Cebīşev de prima speţă pot fi definite recursiv prin : T0(x) = 1, T1(x) = x, Tn+2(x) = 2xTn+1(x) – Tn(x), n ³ 0, sau pot fi definite prin Tn(x) = cos(n arccos(x)). Nodurile Cebīşev sunt proiecţiile pe axa OX a unor puncte egal distanţate situate pe un semicerc:

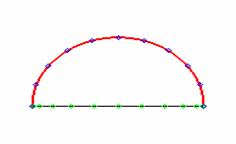
Nodurile Cebīşev au proprietatea că

|(x – x0) (x – x1) … (x – xn)| £

pentru orice xĪ [-1, 1]. Se poate arăta că pentru oricare alte noduri ci, i=0, ...,n.

|(x – c0) (x – c1) … (x – cn)| ³.

Din acest motiv nodurile Cebīşev sunt considerate cele mai bune pentru interpolare. Nodurile Cebīşev pot fi scalate şi translatate pentru a putea fi folosite pe un interval oarecare [a, b]:

xi =  + , 0 £ i £ n.

Astfel īn cazul nodurilor Cebīşev eroarea de interpolare este

| f(x) – Pn(x) | £ .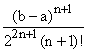

Procedura noduri_echidistante cu parametrii a, b şi n īntoarce lista celor n+1 noduri echidistante din intervalul [a, b]. Pentru n = 0 īntoarce [(a+b)/2].

> noduri_echidistante:=proc(a,b,n)

  if n=0 then RETURN([(a+b)/2]) else RETURN([seq(a+(b-a)/n*i,i=0..n)])

  fi

  end;

Procedura noduri_Cebisev cu parametrii a, b şi n īntoarce cele n+1 noduri Cebīşev corespunzătoare intervalului [a, b].

> noduri_Cebisev:=proc(a,b,n)

  RETURN([seq((b-a)/2*cos((2*i+1)/(2*n+2)*Pi)+(b+a)/2,i=0..n)])

  end;

 

Convergenţa

Fie f : [a, b] ® R şi un şir de diviziuni Dn = (,, …, )  ale intervalului [a, b], n ³ 0. Pentru fiecare n se construieşte polinomul de interpolare Pn asociat nodurilor ,, …,  şi valorilor ,, …, . Se pune problema convergenţei punctuale sau uniforme a lui Pn la f. Īn general, Pn nu converge la f, īnsă dacă f este o funcţie īntreagă reală şirul de polinoame Pn converge uniform la f.

Īn cele ce urmează vom considera trei funcţii f1, f2, f3 : R ® R, definite prin f1 (x) =xcos(x), f2(x) = , respectiv f3(x) = |x|.

> f1:=x->x*cos(x);

> f2:=x->1/(1+x^2);

> f3:=x->abs(x);

Vom vizualiza comportarea polinoamelor de interpolare (sub forma Lagrange) L0, L1,...,Ln asociate unor noduri ,, …,  şi valorilor ,, …,  (cu exemplificări pentru f Ī {f1, f2, f3}).

Procedura grafic_polinoame de mai jos reprezintă grafic n + 1 polinoamele de interpolare L0, L1, ..., Ln. Parametrul tip al procedurii determină ce fel de noduri se vor folosi (n + 1 noduri echidistante dacă tip = 1 şi  n + 1 noduri Cebīşev altfel). Ceilalţi parametri ai procedurii sunt funcţia f (care se aproximează prin polinoame de interpolare), capetele intervalului [a, b] şi n care indică numărul de noduri (n+1).

> grafic_polinoame:=proc(f,a,b,tip,n)

  local xn,yn,titlu,legenda;

  if tip=1 then xn:=[seq(noduri_echidistante(a,b,j),j=0..n)]

  else xn:=[seq(noduri_Cebisev(a,b,j),j=0..n)] fi;

  yn:=[seq(map(f,xn[j]),j=1..n+1)];

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`; x0,  x1,  ..., x`,

  convert(n,string),` noduri `);

  if tip=1 then titlu:=cat(titlu, `echidistante `)

  else titlu:=cat(titlu, `Cebisev `) fi;

  titlu:=cat(titlu, `in intervalul [`, convert(a,string), `,

  `,convert(b,string),`]`);titlu:=cat(titlu,`\ny0=`,f,`(x0), y1=`, f,    

 `(x1), ... , y`,convert(n,string),`=`,f,`(x`,convert(n,string), `)`);

  titlu:=cat(titlu, `\nL i = polinomul de interpolare asociat nodurilor  

  x0,  x1,  ...,x `,convert(i,string),` si valorilor y0,  y1,  ...,y  

 `,convert(i,string),  `,  i =0..`,convert(n,string));

  legenda:=f,seq(cat(`L `,convert(j,string)),j=0..n);

  plot([f(t),seq(polinom_Lagrange(xn[j],yn[j],t),j=1..n+1)],

  t=a..b,labels=[X,Y],color=[COLOR(RGB,1,0,0),seq(COLOR(RGB,(1-

  floor(log[5](j))/(floor(log[5](n))+1))*irem(irem(j,7)+1,2),(1-

  floor(log[5](j))/(floor(log[5](n))+1))*irem(iquo(irem(j,7)+1,2),2),(1-

  floor(log[5](j))/(floor(log[5](n))+1))*irem(iquo(irem(j,7)+1,4),2)),

  j=1..n+1)],thickness=[2,seq(1,j=0..n)],legend=[legenda],title=titlu,

  xtickmarks=map(evalf,xn[n]),ytickmarks=map(evalf,yn[n]));

  end;

 

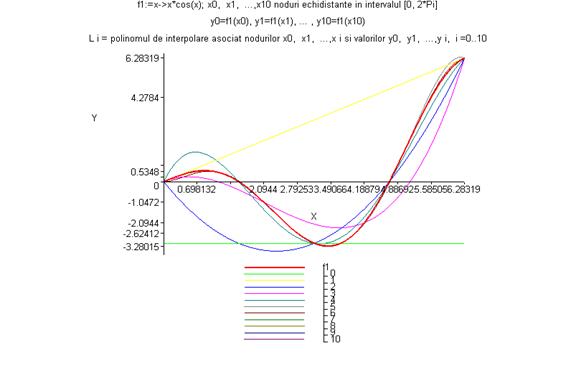
Aplicăm procedura pentru funcţia f1 pe intervalele [0, 2p], [-p, 3p] , funcţia f2 pe intervalul [-3, 3] şi funcţia f3 pe intervalul [-1, 1]. Īn toate cazurile n = 10 şi se consideră două variante: noduri echidistante şi noduri Cebīşev.

> grafic_polinoame(f1,0,2*Pi,1,10);

 

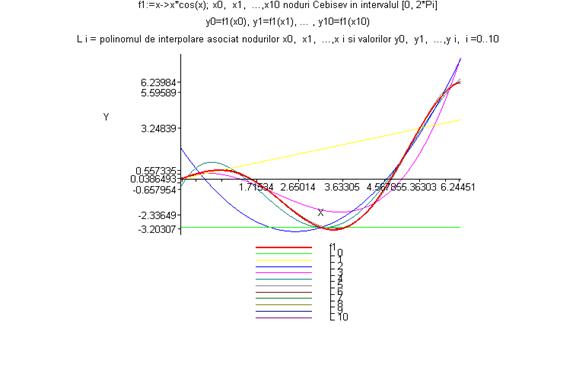
> grafic_polinoame(f1,0,2*Pi,2,10);

 

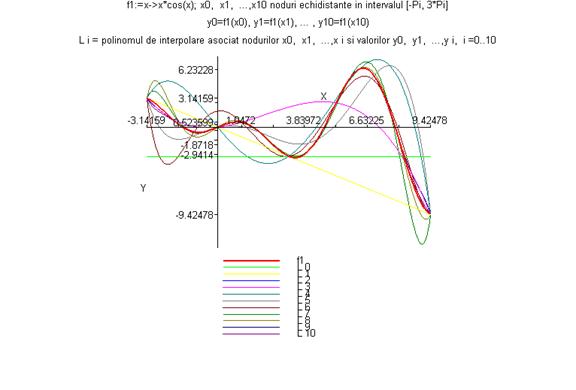
> grafic_polinoame(f1,-Pi,3*Pi,1,10);

> grafic_polinoame(f1,-Pi,3*Pi,2,10);

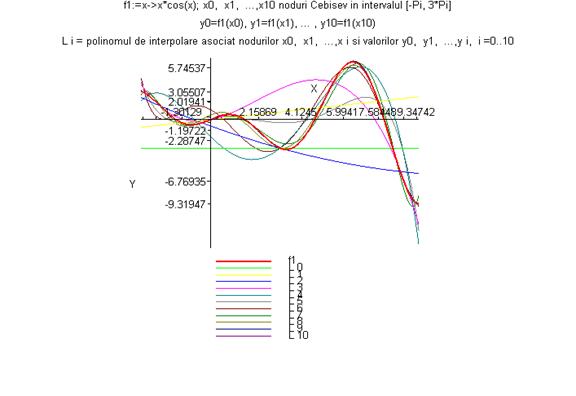
> grafic_polinoame(f2,-3,3,1,10);

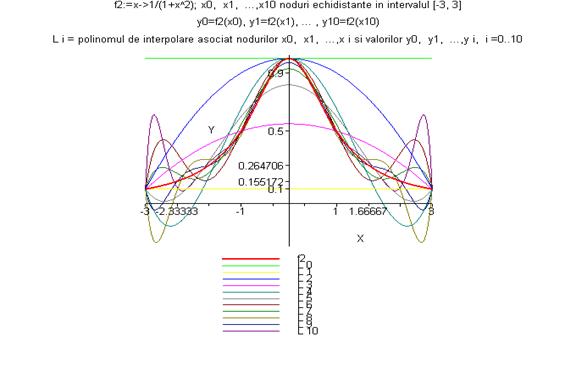
> grafic_polinoame(f2,-3,3,2,10);

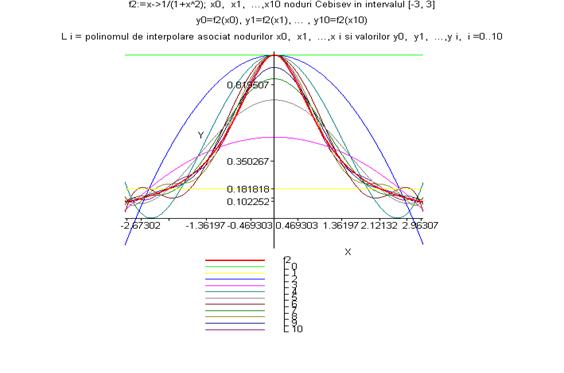
> grafic_polinoame(f3,-1,1,1,10);

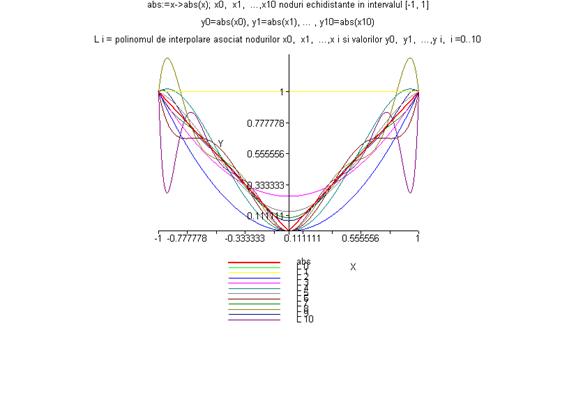
> grafic_polinoame(f3,-1,1,2,10);

 

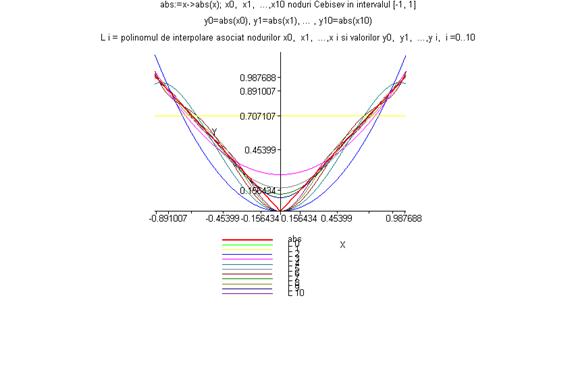
Prezentăm două variante animate ale procedurii grafic_polinoame. Procedura animatie_polinoame1 generează n+1 cadre, īn fiecare cadru i (0 £ i £ n) fiind desenat graficul funcţiei şi al polinomului de interpolare asociat nodurilor ,, …,  (dacă parametrul tip ia valoarea 1, atunci nodurile sunt echidistante, altfel sunt nodurile Cebīşev asociate intervalului [a, b]). Parametrul suplimentar, m, este utilizat drept factor de īncetinire a animaţiei.

 

> animatie_polinoame1:=proc(f,a,b,tip,n,m)

  local xn,yn,titlu,d1,d2,d3;

  if tip=1 then xn:=[seq(noduri_echidistante(a,b,j),j=0..n)]

  else xn:=[seq(noduri_Cebisev(a,b,j),j=0..n)] fi;

  yn:=[seq(map(f,xn[j]),j=1..n+1)];

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`; x0,  x1,  ...,x`,

  convert(n,string),` noduri `);

  if tip=1 then titlu:=cat(titlu, `echidistante `)

  else titlu:=cat(titlu, `Cebisev `) fi;

  titlu:=cat(titlu, `in intervalul [`, convert(a,string), `, `,

  convert(b,string),`]`);titlu:=cat(titlu,`\ny0=`,f,`(x0), y1=`, f,   

 `(x1), ... , y`,convert(n,string),`=`,f,`(x`,convert(n,string), `)`);

  titlu:=cat(titlu, `\nL i = polinomul de interpolare asociat nodurilor

  x0,  x1,  ...,x `,convert(i,string),` si valorilor y0,  y1,  ..., y

  `,convert(i,string),  `,  i =0..`,convert(n,string));

  titlu:=cat(titlu,`\nSe genereaza succesiv polinoamele L0, L1, ...,

  L`,convert(n,string));

  titlu:=cat(titlu,`\nPentru fiecare i, se marcheaza pe graficul

  functiei `,f, ` punctele ( x j, `,f,` (xj) ),  j = 0..i`);

  d1:=plot(f(t), t=a..b,labels=[X,Y],color=COLOR(RGB,1,0,0),

  thickness=2,title=titlu);

  d2:=[seq([seq(pointplot([xn[j][i],yn[j][i]],symbol=circle,

  color=black,thickness=15),i=1..j)],j=1..n+1)];

  d3:=[seq(plot(polinom_Lagrange(xn[j],yn[j],t),t=a..b,labels=[X,Y],

  color=COLOR(RGB,0,0,1),thickness=1),j=1..n+1)];

  display(d1,display([seq(display(d2[j],d3[j])$m,j=1..n+1),

  seq(display(d2[n+1-j],d3[n+1-j])$m,j=1..n)],insequence=true));

  end;

 

       Procedura animatie_polinoame2 generează n+1 cadre, īn fiecare cadru j (0 £ j £ n) fiind desenat graficul funcţiei şi al polinomelor de interpolare asociate nodurilor ,, …,   cu i = 0..j. Dacă parametrul tip ia valoarea 1, atunci nodurile sunt echidistante, altfel sunt nodurile Cebīşev asociate intervalului [a, b]. Parametrul suplimentar, m, este utilizat drept factor de īncetinire a animaţiei.

 

> animatie_polinoame2:=proc(f,a,b,tip,n,m)

  local xn,yn,titlu,d1,d2,d3;

  if tip=1 then xn:=[seq(noduri_echidistante(a,b,j),j=0..n)]

  else xn:=[seq(noduri_Cebisev(a,b,j),j=0..n)] fi;

  yn:=[seq(map(f,xn[j]),j=1..n+1)];

  titlu:=cat(f,`:=x->`,convert(f(x),string) ,`; x0,  x1,  ...,x`,

  convert(n,string),` noduri `);

  if tip=1 then titlu:=cat(titlu, `echidistante `)

  else titlu:=cat(titlu, `Cebisev `) fi;

  titlu:=cat(titlu, `in intervalul [`, convert(a,string), `, `,

  convert(b,string),`]`);titlu:=cat(titlu,`\ny0=`,f,`(x0), y1=`, f,

 `(x1), ... , y`,convert(n,string),`=`,f,`(x`,convert(n,string), `)`);

  titlu:=cat(titlu, `\nL i = polinomul de interpolare asociat nodurilor

  x0,  x1,  ...,x `,convert(i,string),` si valorilor y0,  y1,  ..., y

 `,convert(i,string),  `,  i =0..`,convert(n,string));

 titlu:=cat(titlu,`\nSe genereaza succesiv polinoamele L0, L1, ...,

 L`,convert(n,string));

 titlu:=cat(titlu,`\nPentru fiecare i, se marcheaza pe graficul functiei `,f, ` punctele ( x j, `,f,` (xj) ),  j = 0..i`);

 d1:=plot(f(t),  

 t=a..b,labels=[X,Y],color=COLOR(RGB,1,0,0),thickness=2,title=titlu);

 d2:=[seq(pointplot([seq([xn[j][i],yn[j][i]],i=1..j)],symbol=circle,

 color=black, thickness=15),j=1..n+1)];

 d3:=[seq(plot([seq(polinom_Lagrange(xn[i],yn[i],t),i=1..j)],t=a..b,

 labels=[X,Y],color=[seq(COLOR(RGB,(1-

 floor(log[5](i))/(floor(log[5](n))+1))*irem(irem(i,7)+1,2),(1-

 floor(log[5](i))/(floor(log[5](n))+1))*irem(iquo(irem(i,7)+1,2),2),(1-

 floor(log[5](i))/(floor(log[5](n))+1))*irem(iquo(irem(i,7)+1,4),2)),

 i=1..j)],thickness=[seq(1,i=1..j)]),j=1..n+1)];

 display(d1,display([seq(display(d2[j],d3[j])$m,j=1..n+1),

 seq(display(d2[n+1-j],d3[n+1-j])$m,j=1..n)],insequence=true));

 end;

 

      Procedura animatie_polinoame3 generează n+1 cadre, īn fiecare cadru i (0 £ i £ n) fiind desenat graficul funcţiei şi al celor două polinoamelor de interpolare cu i noduri din intervalul [a, b]: unul corespunzător nodurilor echidistante iar celălalt nodurilor Cebīşev. Parametrul suplimentar, m, este utilizat drept factor de īncetinire a animaţiei. Se poate compara astfel comportarea polinoamelor asociate nodurilor Cebīşev cu cele asociate nodurilor echidistante.

> animatie_polinoame3:=proc(f,a,b,n,m)

  local xn,yn,xnc,ync,titlu,d1,d2,d3,d4,d5;

  xn:=[seq(noduri_echidistante(a,b,j),j=0..n)];

  xnc:=[seq(noduri_Cebisev(a,b,j),j=0..n)];

  yn:=[seq(map(f,xn[j]),j=1..n+1)];

  ync:=[seq(map(f,xnc[j]),j=1..n+1)];

  titlu:=cat(f,`:=x->`,convert(f(x),string),` (grafic desenat cu rosu) ;

  intervalul [`, convert(a,string), `,

  `,convert(b,string),`]`);titlu:=cat(titlu,`\nSe compara polinoamele de  

  interpolare asociate nodurilor echidistante (grafice desenate cu

  albastru)  \n cu polinoamele de interpolare asociate nodurilor Cebisev

  (grafice desenate cu verde)`);

  d1:=plot(f(t),  =a..b,labels=[X,Y],color=COLOR(RGB,1,0,0),thickness=2,  

  title=titlu);

  d2:=[seq([seq(pointplot([xn[j][i],yn[j][i]],symbol=circle,color=black,  

  thickness=15),i=1..j)],j=1..n+1)];

  d3:=[seq(plot(polinom_Lagrange(xn[j],yn[j],t),t=a..b,labels=[X,Y],

  color=COLOR(RGB,0,0,1),thickness=1),j=1..n+1)];

  d4:=[seq([seq(pointplot([xnc[j][i],ync[j][i]],symbol=cross,

  color=black, thickness=15),i=1..j)],j=1..n+1)];

  d5:=[seq(plot(polinom_Lagrange(xnc[j],ync[j],t),t=a..b,

  labels=[X,Y],color=COLOR(RGB,0,1,0),thickness=1),j=1..n+1)];

  display(d1,display([seq(display(d2[j],d3[j],d4[j],d5[j])$m,j=1..n+1),

  seq(display(d2[n+1-j],d3[n+1-j],d4[n+1-j],d5[n+1-j])$m,j=1..n)],

  insequence=true));

  end;

 

Pentru exemplificare: click pe definiţia funcţiilor de mai jos

f1(x) = xcos(x), intervalul [0, 2p]

f1(x) = xcos(x), intervalul [-p, 3p]

f2(x) = , intervalul [-3, 3]

            f3(x) = |x|, intervalul [-1, 1]

 
 
Marian-Silviu Tălmăcel, marianns1@yahoo.com
Oana-Adriana Basarabă
Cristian-Laurenţiu Giorgi, giorgi_cristian@yahoo.com
Roxana-Elena Stăniloiu

 

Studenţi īn anul I la Facultatea de Inginerie, Ingineria Sistemelor
Universitatea Constatin Brāncuşi din Tārgu-Jiu
Bld. Republicii, Nr. 1, 210152 Tārgu-Jiu, Romānia.
 
Lucrare prezentată la sesiunea de comunicări ştiinţifice studenţeşti din cadrul concursului naţional de matematic㠄Traian Lalescu”, Universitatea Politehnică Bucureşti, 30 mai – 1 iunie 2008.